Comparisons: Introduction (Single-Winner)

In the Evaluations (Ranked Ballot) chapter, CHPV is assessed against the various independent voting system criteria to highlight its own unique strengths and weaknesses. In this chapter, ranked ballot CHPV is compared in turn to a variety of other single-winner voting systems to assess which is the better method given certain election profiles or scenarios.

Ranked Ballot CHPV versus other Single-Winner Voting Systems

As CHPV is a positional voting system, it is initially compared to the plurality and Borda Count methods. The Borda Count is a classic positional system that employs a linear distribution of points from N points for the first preference down to one point for the last preference. The single-round first-past-the-post (FPTP) version of plurality is not strictly a positional voting system but it can be viewed as such where a first preference is worth one point and all subsequent preferences are worth nothing (zero points).

For GV with a first preference weighted as one and a common ratio of zero, all the lower preferences are hence weighted as zero. Therefore, GV with r = 0 equates to FPTP. At the other extreme, the common ratio can approach one (r → 1) but cannot quite equal it; as r = 1 is invalid. It is demonstrated later that this GV variant is equivalent to the Borda Count in terms of the collective candidate rankings; see the Comparisons: Borda Count 3 page.

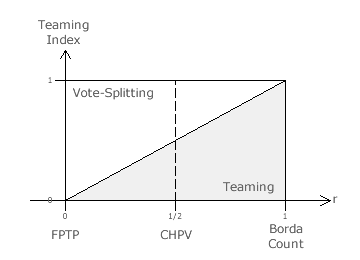
Firstly, CHPV is directly compared to FPTP and then the Borda Count. Next, CHPV is compared to other GV variants on a spectrum that varies from FPTP to the Borda Count as the common ratio (r) is varied from zero towards one. This range encompasses all possible three-candidate positional voting system outcomes.

It is well-known that FPTP suffers from vote splitting but not teaming. Conversely, the Borda Count suffers from teaming but not vote splitting. As the common ratio (r) used in a GV variant increases, the degree to which it is vulnerable to vote splitting decreases while the degree to which it is vulnerable to teaming increases; see graph opposite.

CHPV is the central GV variant that achieves a balance between these two conflicting features. From the evaluation of GV, recall that for r ≤ 1/2 voters can always thwart teaming attempts. Therefore, CHPV is the furthest GV variant from FPTP and the closest to the Borda Count that minimises vote splitting yet always enables teaming attempts to be thwarted.

CHPV is also compared to other preferential voting systems but ones that do not use positional algorithms. Condorcet methods employ pairwise comparisons of preferences to determine election outcomes so they differ sharply with CHPV results. CHPV is further compared to the alternative vote (AV); also known as instant run-off voting (IRV). Here, the winner requires over 50% support and this is often determined following the transfer of votes from eliminated candidates.

The various preferential methods differ in terms of which preferences are influential in deciding the winner and whether all preferences count towards this decision. For FPTP only first preferences count and for AV only the top preferences matter (after each candidate elimination). Hence, most preferences (the lower ones) are ignored and unsurprisingly both FPTP and AV favour polarized candidates over consensus ones.

In contrast, for the Borda Count and Condorcet methods each and every preference counts towards the election result. As differences between adjacent high preferences and between adjacent low preferences are treated alike, they strongly favour consensus candidates over polarized ones. For the Borda Count, the winner is the one with the best average preference.

CHPV also employs every preference expressed by each voter. However, CHPV does not focus on the best average preference nor just on the top preferences so it does not especially favour consensus or polarized candidates. Instead, it emphasises the need for candidates to acquire 'high' preferences; those weighted above the mean. The winner in a CHPV election needs to have a sufficiently broad array of such preferences for victory.

In the final section, the plurality rule is introduced as a complementary alternative to the majority rule. Put simply, the plurality rule ensures that the option with the best overall tally wins rather than the one that - having the better tally - wins the most pairwise comparisons. Methods that use the plurality rule can then be subdivided according to whether they might need more than one round of counting to produce a result. The single-round or direct methods do not require the winner to have a majority of the tallies; just a plurality. In contrast, the multiple-round or iterative methods do require winners to have both a plurality and a majority by the final round.

Examples of iterative plurality rule methods include exhaustive and two-round plurality, the supplementary vote, Coombs method and Bucklin voting. Approval and range voting are examples of direct plurality rule methods. They are all briefly described and compared to CHPV which, as a positional voting system, is also a direct plurality rule method.

Proceed to next section > Comparisons: Plurality (FPTP)

Return to previous page > Evaluations: Summary (Party-List)