Description: Weightings

The formal definition of GV and CHPV weightings now follows and it inevitably involves some simple mathematics. For this Description chapter, it is not critical reading. Therefore, this page may be skimmed over or skipped completely as the remaining sections of the chapter can still be understood with just a very basic knowledge of arithmetic. For visitors wishing the progress to the Evaluations and Comparisons chapters later, this page is however essential reading.

Geometric Voting (GV) is a class of preferential and positional voting systems that employ a decaying geometric progression of preference weightings for the sequence of descending rank order positions.

Consecutively Halved Positional Voting (CHPV) is GV with a common ratio of one half.

The following statements define some of the various parameters of GV:

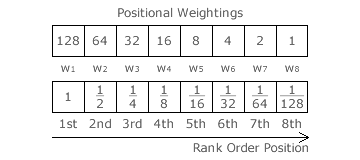
N = Number of preferences/candidates/options

P_n = nth Preference where 1 ≤ n ≤ N

r = common ratio where 0 ≤ r < 1

a = weighting of first preference (P₁) where a > 0

w_n = weighting of nth preference (P_n)

w_N = weighting of last preference (P_N)

The upper row in the table opposite shows the preference weightings for an example ranked ballot GV election with eight candidates (N = 8), a common ratio of one half (r = ½ ⇒ CHPV) and a last (8th) preference weighting of one (so a = 128). For comparison, the lower row in the table has an initial weighting of one (a = 1) instead.

It directly follows from the above statements that:

w₁ = a

w₂ = a x r = ar

w₃ = a x r x r = ar²

w₄ = a x r x r x r = ar³

w_n = a x r x r x r ... = ar^n-1

w_N = a x r x r x r ....... = ar^N-1

The table opposite displays these specific weightings for the first, second, third, fourth, nth and last (Nth) preferences in rank order for any ranked ballot GV election.

Note that the weighting of any preference can be obtained by multiplying the preceding preference by the common ratio. Namely, that w_n+1 = r x w_n. Rearranging yields r = w_n+1 ÷ w_n. In other words, the common ratio is the relative weight of any given preference with respect to its adjacent higher-ranked preference. The choice of common ratio has a crucial impact on any election outcome but the initial weighting (w₁ = a) has no effect at all on candidate ranking since it is a common scaling factor in every positional weighting.

As demonstrated on the previous page, each CHPV preference weighting is equal in value to the sum to infinity of all lower preference weightings. As the first preference (w₁ = a) is therefore worth the same as the total of all the remaining ones, then the sum of all CHPV weightings is a + a or 2a. In practice, for a finite but still large number of candidates or options, this sum will closely approximate to this value of 2a. The precise difference between the actual sum and the infinite sum - the remainder - will always be equal in value to the weighting of the last preference (w_N = ar^N-1).

For party-list GV elections, let the tally of votes cast for party A be T_A. Also, let the first or top candidate on the list for party A be A₁, the second be A₂, the third A₃ and so on. The tally awarded to the top candidate is generally the same as the tally achieved by the party itself; namely, T_A1 = T_A. For a candidate placed nth on the party list, their personal tally is consequently T_Ar^n-1. For party-list CHPV elections, party A candidates A₁, A₂, A₃, A₄ and so on hence have tallies of T_A, T_A/2, T_A/4, T_A/8 and so on respectively.

Proceed to next section > Description: Voting

Return to previous page > Description: Analogy