Comparisons: Sainte-Laguë ~ Proportionality 2

Sainte-Laguë Domain Centres (continued)

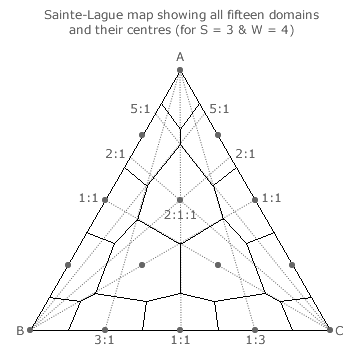
Unlike for two-party elections, with three or more competing parties, outcomes are not always optimally proportional. So, consider the example three-party map opposite where all its fifteen domains and their centres for a four-winner election are illustrated.

For the 2:1:1 seat share domain, three two-way tie lines are also shown (as dotted lines) intersecting with each of the three apexes. In each case, the relevant critical sections of the outer pair form two opposing sides of the irregular hexagonal domain. The two-way tie line that intervenes between each outer pair exactly bisects the angle between these two lines. The bisecting lines from the three apexes all intersect at the same point; namely, at the centre of the domain.

The tally shares for the 1:1 tie line are 1/2 (or 3/6) each for parties A and B when party C has zero. For the 5:1 tie line, they are respectively 5/6 and 1/6. Hence, for a tie line to bisect the intervening angle, they are required to be 4/6 and 2/6 respectively. This bisecting line therefore represents a tally share ratio for A:B of 4:2 or 2:1 as shown. The other two bisecting lines are similarly determined to have ratios of 2:1 for A:C and 1:1 for B:C. The tally share ratio for the 2:1:1 seat share domain centre is hence 2:1:1.

For this non-peripheral domain, its centre is perfectly located with no offset relative to its corresponding OPV domain centre.

This also applies to every non-peripheral domain on any three-party map. Further, all the centres of such domains are therefore uniformly distributed across the map with a fixed distance from one centre to any of its (up to six) neighbouring centres; see the earlier Sainte-Laguë Method ~ Maps 2 and Sainte-Laguë Method ~ Maps 3 pages.

As with the two-party maps, this uniform spacing also applies to the centres of the peripheral domains. They are hence located on the edges of the map for edge domains or at the apexes of the map for corner domains. Notice that the area of edge domains and corner domains is one half and one sixth that of non-peripheral domains respectively.

Regardless of the number of winners or of competing parties, the regular spacing of all the domain centres on a map and the extreme positioning of the peripheral ones means that no disproportionality is introduced by the Sainte-Laguë algorithm; at least in terms of domain centres and the voting system least squares index (LSI_VS).

• Therefore, LSI_VS = 0 for any multiple-party multiple-winner Sainte-Laguë election.

The Hare Quota Party-List voting system also has a LSI_VS of zero. However, unlike the Hare Quota method with its regular hexagonal domains, the tally shares at a non-central point in an irregular hexagonal Sainte-Laguë domain may not always yield an optimally proportional result. Hence, despite having the same disproportionality index, the Hare Quota is a more proportional system than the Sainte-Laguë method.

Party Proportionality of the Sainte-Laguë, D'Hondt and CHPV Methods

Party-list CHPV can now be compared to the Sainte-Laguë method in terms of both disproportionality and optimality (see earlier section). In both respects, the Sainte-Laguë method clearly outperforms CHPV irrespective of the number of winners or parties in a party-list election. However, CHPV is much less susceptible to party cloning than is the Sainte-Laguë method.

The Sainte-Laguë method is more party proportional than the D'Hondt method. Indeed, it is the most party proportional of all the highest averages approaches. With only a few winners, CHPV is ranked between these two methods. In terms of party cloning, the D'Hondt method is not as vulnerable as the significantly susceptible Sainte-Laguë method. Again, with only a few winners, CHPV is ranked between these same two methods.

For these three highest averages approaches, there is the inherent trade-off between party proportionality and susceptibility to party cloning. Provided concurrent elections are held in multiple few-winner constituencies, party-list CHPV minimises this conflict. With no more than five winners, CHPV is not susceptible to a minority party attempting to gain an unfair advantage through cloning. Yet, with around five seats, it is at its peak in terms of optimally proportional outcomes.

Proceed to next section > Comparisons: Mixed Member Systems

Return to previous page > Comparisons: Sainte-Laguë ~ Proportionality 1