Mathematical Proofs: Positional Voting

Proof CV5: Bias Indices and Truncation

Using a geometric voting vector, the effect on the two bias indices of truncating the last preference weighting (w_N = r^N-1) to become zero (w_N = 0) can be determined. The standard form of the GV(r) vector, its normalized version and its truncated one are all stated below. Note that the truncated vector automatically becomes normalized.

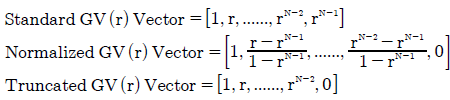
The sum of all the normalized preference weightings for the untruncated vector U (Σ_U) and for the truncated vector T (Σ_T) must be calculated before either bias index can be deduced. These two sums are each specific to the actual vector employed by the voting system. However, it is shown below that regardless of the particular vector chosen, the truncated vector T always has a larger sum than its untruncated vector U.

As both vectors are normalized, the first preference (w₁ = 1) and the last preference (w_N = 0) have been set to the same weighting in each vector. The intermediate preferences with rank positions from second to penultimate (2 ≤ n ≤ N-1) need to be individually compared at each rank position to determine which one is the greater of the two. Let k be the comparison factor for the untruncated vector relative to the truncated one; namely k = w_n(U)/w_n(T). Consequently, as shown below, k is always less than one and the intermediate weighting of rank n in the truncated vector is hence always greater than its corresponding one in the untruncated one.

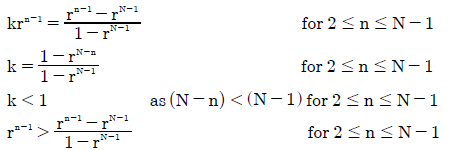
So w_n(T) > w_n(U) for any and indeed every intermediate preference of rank n. As each intermediate weighting in the truncated vector T is always greater than each corresponding one in the untruncated vector U, then for the two sums of these weightings Σ_T must always be greater than Σ_U for any chosen vector. The following relationship between the two polarization indices and between the two consensus indices is therefore established.

While the magnitude of the shift in either index is specific to the particular GV(r) vector chosen, the direction of this shift when truncation of the last preference weighting occurs is consistently in favour of greater consensus, and so less polarization.

Return to main text > Comparisons: Positional Voting 9

Refer to > Mathematical Proofs: Table of Contents