Mathematical Proofs: General Criteria
Proof EG1: GV (any r) fails the Condorcet Winner Criterion

Where one candidate in a particular election beats each and every other candidate in a pairwise comparison, then this candidate is called the Condorcet Winner. If the voting system ensures that the winning candidate is always the Condorcet Winner (if there is one) irrespective of the election profile or voter input, then the Condorcet Winner criterion is satisfied and the voting system is classed as a Condorcet method.
To prove that GV with any valid common ratio (0 ≤ r < 1) fails to satisfy this criterion, only one example scenario is required; see table opposite. If the Condorcet Winner fails to be ranked top in this GV (any r) election, then the voting system fails to ensure that the Condorcet Winner always wins and therefore this criterion is not satisfied.
In a pairwise comparison of the ballots cast by the V voters, the fraction 1/2 - α of these ballots prefer candidate A to C (the type 1 ballots) but the fraction 1/2 + α prefer C to A (the type 2, 3 and 4 ballots). Similarly, candidate C is preferred to B by the same +2α margin. Hence, as one candidate beats all the other (two) candidates in the pairwise comparisons, there is a Condorcet Winner here and it is candidate C.
To prove that GV (any r) fails to satisfy the Condorcet Winner criterion, this example scenario only needs to demonstrate that candidate C never wins whatever the common ratio employed. The tally (TA) for candidate A and the tally (TB) for B are always equal as these two tied candidates have the same number of preferences at each rank position. The tally (TC) for candidate C must always be less than the one for A or B if C is to lose this GV (any r) election.
The three candidate tallies are determined below from the data contained in the above table. Each tally is then divided by the total number of ballots (V) to yield the average tally contribution per voter for that candidate. For this proof, the fraction α tends to zero (α → 0); namely one vote in an unlimited number of votes (V → ∞).
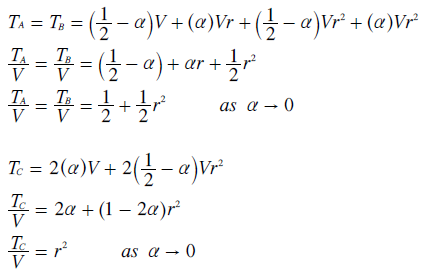
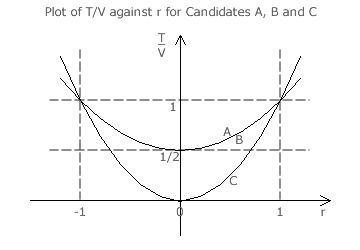
The average tally contribution (T/V) for each of the three candidates is plotted on the graph opposite as a function of the common ratio (r). For this plot, the fraction α is treated as zero. By inspection, the value of T/V for candidate C only exceeds that for A or B when r has a magnitude of about 1 or higher. A magnitude of 1 or more for r is simply invalid. A negative sign for r is also invalid. So, from the graph, the only possible valid values for r where the Condorcet Winner might be elected are just under +1.
To accurately determine the maximum value of r that ensures that C loses the election, the average tally contribution for A or B (TA/B/V) is directly compared to that for C. This comparison and the resultant quadratic equation are given below. The standard mathematical formula for solving a quadratic equation is then employed to derive the two values for r where C is on the verge of winning.
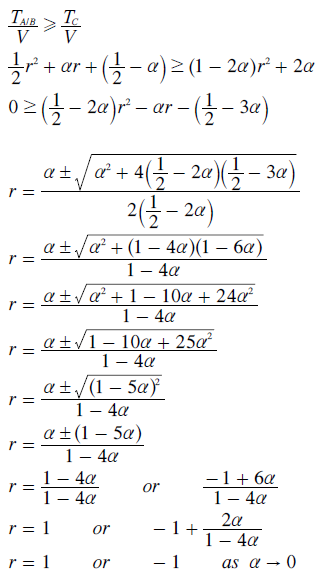
The negative value of r is not quite equal to -1 but it is still negative and hence invalid. The positive value of r is exactly +1 regardless of the value of α and so is also invalid. Hence, there is no valid value of r whereby the tally for C exceeds that for A or B. So the Condorcet Winner C loses this GV election to the tied candidates A and B whatever the common ratio employed.
- Therefore, GV (any r) fails the Condorcet Winner criterion.
Return to main text > Evaluations: General Criteria 3
Refer to > Mathematical Proofs: Table of Contents
