Mathematical Proofs: Positional Voting

Proof CV2: Common Ratio for Anti-GV(r) Vectors

This proof for anti-vectors closely follows the corresponding ones for vectors. Hence, results from proof CG1, proof CG2 and proof CG3 are often restated here rather than being reworked. Reference back to any of these proofs may be made as necessary.

The weightings of the preferences P₁, P₂ and P₃ of a GV(r) vector are respectively w₁, w₂ and w₃. Since the three map co-ordinates sum to unity, they are a, b and c where a = w₁/W, b = w₂/W and c = w₃/W and W = w₁ + w₂ + w₃.

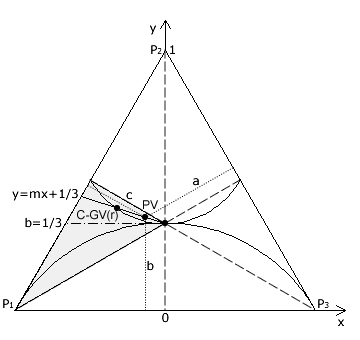
Conjugate vectors may also be plotted on a three-preference map; see opposite. The weightings for any conjugate C-GV(r) vector (u₁,u₂,u₃) are u₁ = 1 - w₃/W, u₂ = 1 - w₂/W and u₃ = 1 - w₁/W where W is the sum of the components of GV(r) vector (w₁,w₂,w₃). The common ratio here for conjugate vectors is defined as r = w₂/w₁. As these conjugate weightings sum to two, the corresponding three-preference map co-ordinates here are now a = u₁/2 = (1 - w₃/W)/2, b = u₂/2 = (1 - w₂/W)/2 and c = u₃/2 = (1 - w₁/W)/2. The point C-GV(r) on the map opposite represents this conjugate vector and its corresponding A-GV(r) anti-vector.

The expressions for these preference co-ordinates may be rearranged such that each one is a function of the sum of two of the weightings as demonstrated below:

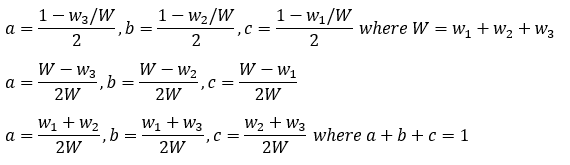
The relevant map co-ordinates for any conjugate vector C-GV(r) are therefore as stated below:

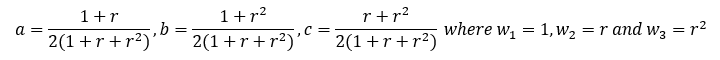
The cartesian co-ordinates x and y for any point on the preference map are derived in proof CG1 and repeated below. By substituting the three C-GV(r) map co-ordinates a, b, and c into the equations for x and y, the relationship between them and the common ratio is established; see below.

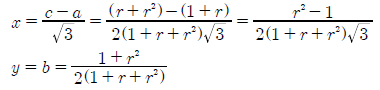
In proof CG1 it is demonstrated that the circular arc of GV(r) vectors is part of a circle of radius 2/3 and centred at x = 0 and y = -1/3. The circular arc for C-GV(r) vectors is instead formed by part of a circle with radius 1/3 and centred at x = 0 and y = +2/3. Using the equation R² = X² + Y² for a circle again, the following proof of this statement is provided.

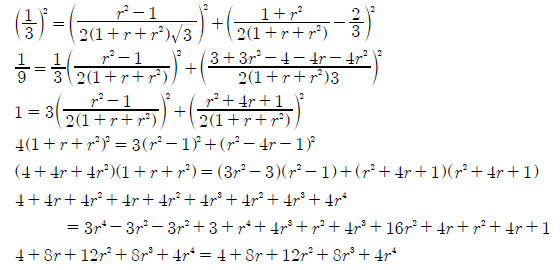
As the equality is established, the arc of the C-GV(r) vectors is indeed as shown on the above map.

In proof CG2 it is shown that a straight line within the valid ranking region from the edge of the map to its centre represents equivalent positional voting systems in terms of collective candidate rankings. Further, in proof CG3 the value of the common ratio is derived for a GV(r) vector that may replace the other vectors represented by the points along this line. Using the equation y = mx + 1/3 for the straight line again, the common ratio for a C-GV(r) vector equivalent to another positional voting conjugate vector - such as PV in the above map - is determined as follows.

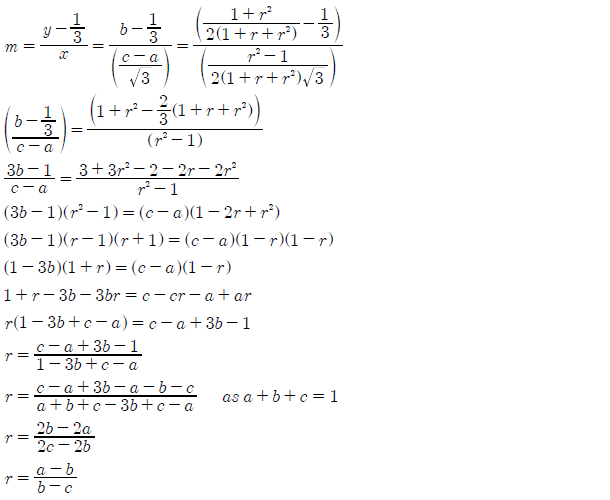
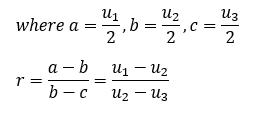
• For any valid positional voting conjugate vector (u₁,u₂,u₃), there exists an equivalent C-GV(r) and A-GV(r) vector where the value of its common ratio is r = (a-b)/(b-c) = (u₁-u₂)/(u₂-u₃).

Note that the common ratio here is the difference between the first and second preference weightings divided by the difference between the second and third preference weightings. For ordinary vectors, the numerator and denominator are transposed for this division.

Return to main text > Comparisons: Positional Voting 4

Refer to > Mathematical Proofs: Table of Contents