Mathematical Proofs: Positional Voting

Proof CV6: Consensus and Polarization Indices for Truncated GV(r) Vectors

The standard positional voting vector for geometric voting with a common ratio of r is given below.

This vector following truncation of its last preference from w_N = r^N-1 to w_N = 0 is shown below.

The formula for calculating each bias index is given in the Consensus and Polarization Indices for Positional Voting Vectors proof. It is however useful to determine the sum of all the preference weightings first. Geometric voting derives its name from the fact that its preference weightings form a geometric progression. As such, the standard mathematical formula for determining the sum of the first N-1 terms in a geometric progression is used here. Note that the Nth term is zero.

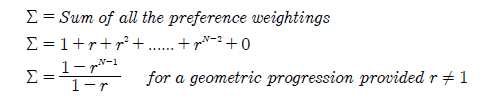
Notice that the sum Σ is a function of both the common ratio r and the number of candidates N. Hence, the two bias indices are also functions of these variables; see below

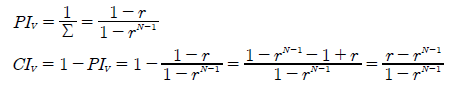
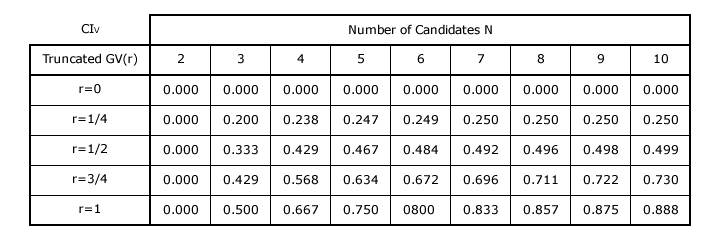
The table below gives the Consensus Index (CI_V) value for the truncated GV(r) vector for selected values of r up to ten candidates. The corresponding table for the untruncated version is given in proof CV2.

As the number of candidates tends to infinity (N → ∞), the sum Σ simply reduces to 1/(1-r). Therefore, the two bias indices can be greatly simplified here as shown below.

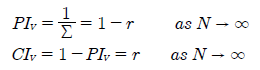
As the number of candidates (N) increases, the Consensus Index (CI_V) for a truncated GV(r) vector - like that for the untruncated vector - converges towards its asymptote. However, for N > 2 and r > 0, this index is consistently closer to its asymptotic value of r with the truncated vector (_TV) rather than the untruncated vector (_UV). The table below gives the difference in consensus index values (CI_TV - CI_UV) between the two.

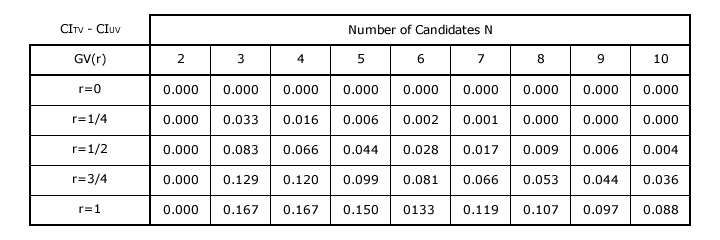
Notice that the non-zero values in the above table are all positive. This demonstrates that the untruncated vector never has a consensus index closer to its asymptotic value (r) than the truncated version. In a large field of candidates (especially when N → ∞) the difference in these two indices is minimal. If however, it is desired for the system bias to remain close to CI_V = r in a relatively small field of candidates, then the truncation of any GV(r) vector such that w_N = 0 will significantly advance this objective.

Therefore, when designing a positional voting system to exhibit a specific bias without prior knowledge of the number of candidates that will be nominated, this is essentially achieved by selecting the appropriate common ratio for the vector such that r = CI_V = 1 - PI_V and truncating its last preference weighting to w_N = 0.

Return to main text > Comparisons: Positional Voting 10

Refer to > Mathematical Proofs: Table of Contents