Comparisons: Positional Voting 10

Designing Systems for a Specific Bias

Only the Plurality vector has a fixed system bias irrespective of the number of candidates (N) standing. It is wholly polarized. For a vector with maximum consensus regardless of N, then the Borda Count should be employed. For a relatively large field of candidates, the analysis in proof 3 and on page 5 and page 7 highlights that the bias of a positional voting system can largely be fixed by adopting a GV(r) vector where r = CI_V when N → ∞. Also, the analysis in proof 5 and on page 8 shows that last place truncation raises the CI_V closer to its asymptotic value of r. The table below illustrates the scale of this shift for the CHPV vector (CI_V ≈ r = 0.5). With relatively few candidates, truncation has a marked beneficial effect.

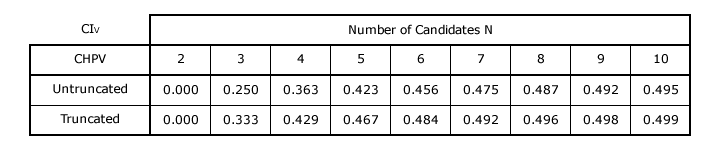
For a small field of candidates, it is not possible to design a positional voting system with a fixed bias without knowing beforehand how many candidates will actually stand. However, unless N is especially small, the best option is typically to use a GV(r) vector with the requisite common ratio and the lowest rank position truncated.

To design a balanced or unbiased system for any number of competing candidates, CHPV should be chosen since its common ratio r = 1/2 and its CI_V ≈ PI_V; thus the bias in each opposing direction is essentially negated by the other. Truncating this vector improves adherence to its inherent lack of bias towards either consensus or polarization. However, it must be borne in mind that in so doing the other key properties of CHPV may be somewhat adversely affected. Last place truncation is more important and effective when designing a positional voting system with a bias towards consensus rather than polarization.

• For balanced (unbiased) N-candidate positional voting, a lowest-rank truncated CHPV vector is optimal.

Proceed to next section > Comparisons: Condorcet Methods

Return to previous page > Comparisons: Positional Voting 9