Comparisons: Positional Voting 2

Intensity of Differences between Adjacent Preferences

Before searching for whole vector indices, those for adjacent preferences can be used to highlight their comparative significance. Many rival single-winner methods only permit the ranking or pairwise comparison of candidates without voters conveying the strength of any differentiation between them. However, with positional voting and equivalent systems the chosen vector imposes an implied intensity between adjacent rank positions regardless of actual voter perceptions.

The CI_L index is the value of the lower preference relative to the adjacent higher one. For GV(r=0), there is no value to any lower preference as CI_L = r = 0. This is most unlikely to reflect the sincere views of any voter. The PI_L index is the difference between the two preferences again relative to the higher one. For GV(r→1), PI_L values will be minimal especially with a large field of candidates. This implies that there is little to distinguish between any two adjacently placed candidates regardless of their rank. Again, this imposition is most unlikely to reflect genuine voter opinions.

A reasonable compromise between worthless candidates (CI_L = 0) and barely indistinguishable ones (PI_L → 0) would be to adopt a more centrist view around CI_L = PI_L = 1/2. Before normalization, the geometric progression of CHPV weights as rank increases constitutes a discrete natural (exponential) decay function that exactly meets this requirement. As the field of candidates shrinks from large to small, the process of normalization will gradually distort these index values somewhat but a roughly central compromise is retained. CHPV is still much more likely to be closer to voter opinions on the comparative worth of candidates than the extremes of GV(r=0) [≡ First-past-the-post] or GV(r→1) [≡ Borda Count rankings]. Unlike either extreme, discrimination between adjacent candidates when using CHPV becomes greater as they rise in rank.

Defining the Consensus and Polarization Indices for a Voting Vector

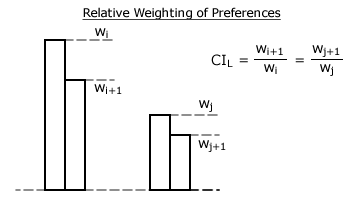
So far, only two adjacent preferences have been used to generate the two bias indices. For an entire voting vector, all such adjacent pairs of preferences should somehow be included within its Consensus Index (CI_V) and Polarization Index (PI_V). Remember that the CI_L ratio w_n+1/w_n represents the relative (not absolute) value of the lower preference with respect to the higher one.

Also in relative terms, a high-ranked preference within the vector should be awarded greater importance than a much lower-ranked one. Taking the arithmetic or geometric mean of all the index values would give unwarranted equal weight to every preference rank whether high or low. Therefore, a weighted average of all the preference-pair consensus indices for the vector is employed instead.

In the figure above, the CI_L for the ith and jth preference pairs are the same. However, as w_j is much smaller than w_i, preference j should be weighted correspondingly less than preference i. As each CI_L is determined with respect to the higher preference, then this preference is again used to weight each CI_L. Using this preference also avoids the prospect of later division by zero. The bias indices for the voting vector can now each be determined as the weighted average of all the relevant preference-pair indices that comprise the vector. The consensus and polarization indices are defined below for a normalized vector with w₁ = 1 and w_N = 0.

• CI_V = (Σ - 1)/Σ       where Σ = Sum of all the normalized vector preference weightings
• PI_V = 1/Σ

Note that the range for Σ is 1 ≤ Σ ≤ ∞ as w₁ = 1 regardless of the other weightings. The index ranges are hence 0 ≤ CI_V ≤ 1 and 0 ≤ PI_V ≤ 1. So each index covers the whole consensus-polarization spectrum from one extreme to the other.

If the above consensus and polarization indices are meaningful and definitive guides to the biases of the various positional voting systems, then they must accord with the established nature of existing vectors such as Plurality and the Borda Count. There is no more polarized system than Plurality (First-Past-The-Post) or GV(r=0). Similarly, there is no more consensual vector than the Borda Count or GV(r→1). For the Plurality vector, the sum of all its weightings is simply one (Σ = w₁ = 1). As the Borda Count vector forms an arithmetic progression from w₁ = 1 to w_N = 0, the sum of any such progression is (w₁+w_N)N/2 or simply N/2 here, so this sum can range from one to infinity (1 ≤ Σ ≤ ∞). The resultant consensus and polarization indices for the Plurality and Borda Count vectors are given below where CI_V = 1 - PI_V.

• Plurality:        PI_V = 1/Σ = 1/1 = 1                   and CI_V = 1 - 1 = 0
• Borda Count:   PI_V = 1/Σ = 2/N (= 0 as N → ∞)     and CI_V = 1 - 2/N (= 1 as N → ∞)

As required, Plurality is confirmed as a wholly polarized vector regardless of the number of candidates (N). When N = 2, all voting vectors including the Borda Count produce the same outcome; namely that the more popular one wins. Therefore, all vectors are entirely polarized with only two candidates standing. As more candidates compete, the consensus index for the Borda Count rises rapidly and asymptotically approaches one (CI_V → 1). Hence, for a large finite field of candidates, the Borda Count is almost wholly consensual. So, depending on N, its consensus index is in the range 0 ≤ CI_V < 1.

Proceed to next page > Comparisons: Positional Voting 3

Return to previous page > Comparisons: Positional Voting 1