Comparisons: Positional Voting 3

Anti-Vectors and Conjugate Vectors

Plurality is where each voter casts a preference for just one candidate. Anti-Plurality is so-called because each voter casts a preference against a single candidate. The normalized Plurality vector is [1,0,...,0]. However, for the Anti-Plurality one there is a choice of two definitions; either [0,...,0,-1] or [1,...,1,0]. Adding one to each and every weighting changes the candidate tallies but not their resultant rank order. Unfortunately, the weightings sum of the first definition (-1) differs from that of the second one (N-1) and it is this sum that determines the bias indices. Therefore, which one - if either - should be employed? In order to address this problem, let the two types of 'anti' vectors be defined as follows:

• For Vector [w₁, w₂, ..., w_N-1, w_N], let its Anti-Vector be [-w_N, -w_N-1, ..., -w₂, -w₁]
• For Vector [w₁, w₂, ..., w_N-1, w_N], let its Conjugate Vector be [1-w_N, 1-w_N-1, ..., 1-w₂, 1-w₁]

Vectors, as here, are usually normalized such that w₁ = 1 and w_N = 0. Hence, for anti-vectors, the first and last preferences are weighted as 0 and -1 respectively. However, conjugate vectors, like ordinary vectors, are normalized such that first and last preferences are weighted 1 and 0 respectively. Notice that as the sum of all the weightings for a vector is Σ, then this sum is -Σ for an anti-vector and N-Σ for a conjugate vector.

Every normalized vector has its 'anti' version so what is the corresponding anti-vector and conjugate vector for the Borda Count? For the vector [1, 1-d, 1-2d, ..., 2d, 1d, 0], its anti-vector is [0, -d, -2d, ..., 2d-1, d-1, -1] and its conjugate vector is [1, 1-d, 1-2d, ..., 2d, 1d, 0]. Note that the Borda Count vector and its conjugate (Anti-Borda Count) are identical. Therefore, both have the same bias indices and the same sum (Σ = N/2). Plurality (where Σ = 1 and PI_V = 1) is the most polarized voting system and the Borda Count (where Σ → ∞ and PI_V → 0 as N → ∞) is the most consensual one across the range of vectors.

For Anti-Plurality, its anti-vector is [0, ..., 0, -1] and its conjugate vector is [1, ..., 1, 0]. Either version may be used in practice as both yield identical candidate rankings since the difference between corresponding weightings is unity in all cases. Hence both exhibit the same system bias but the sum of all the weightings is -1 for this anti-vector yet N-1 for its conjugate version. Since the conjugate vector for Anti-Plurality and the ordinary vector for Plurality are both normalized with the first and last preferences weighted as 1 and 0 respectively then it is their weightings sums that define Σ for the calculation of system bias. Therefore, the full range of Σ from 1 through N/2 to N-1 spans from Plurality (where Σ = 1) through the Borda Count and the Anti-Borda Count (where Σ = N/2 for both) to Anti-Plurality (where Σ = N-1). As the sum Σ increases across this range, then the vectors steadily become less polarized and more consensual. So, Anti-Plurality is the most consensual positional voting system and Plurality the most polarized.

Examples of Vectors, Anti-Vectors and their Bias Indices

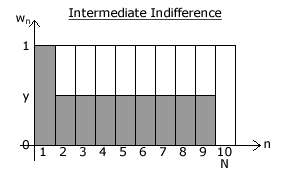
An 'Intermediate Indifference' vector or conjugate vector may be defined by [1, y, y, ..., y, y, 0] as illustrated opposite where the number of candidates (N) is ten and y = 1/2. For equivalence to Plurality, y should be set to zero or, for equivalence to the conjugate version of Anti-Plurality, y should be set to one instead. Hence, the PI_V for this vector will decrease from 1 to 1/5 (since Σ = N/2) as y rises from 0 to 1/2. As y rises further from 1/2 to 1, the PI_V for this (now) conjugate vector will decrease further from 1/5 to 1/9 (since Σ = N-1).

At the mid-point where y = 1/2 and Σ = 10/2 = 5, note that the bias indices are the same as for the Borda Count where Σ = N/2 too. However, although they share the same system bias, other features of these two vectors will differ and different candidate rankings should be expected.

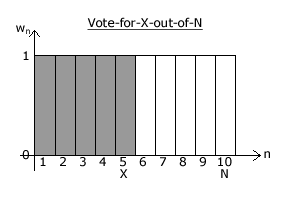
Another example case is that of the 'Vote-for-X-out-of-N' vector or conjugate vector. For X = 5 and N = 10 (as illustrated opposite), the vector is defined by [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]. By varying X from 1 (Plurality) to 9 (Anti-Plurality) in steps of one, the PI_V of this vector also rises from 1 to 1/5 and then for the conjugate vector from 1/5 to 1/9.

Again, at the mid-point its bias indices are the same as for the Borda Count. All positional voting systems will share the same bias indices if they also share the same sum Σ. Again, it will be their other features that distinguishes one vector from another.

Proceed to next page > Comparisons: Positional Voting 4

Return to previous page > Comparisons: Positional Voting 2